How to Play Sudoku
Sudoku is a logic game played on a 9x9 grid using the digits 1 through 9.
This grid is further subdivided into nine 3x3 boxes. The goal is to fill in
the grid with digits such that one and only one of each digit 1 through 9
appear in every row, column, and box.
At logicgamesonline.com, you enter a digit in a sudoku grid cell by moving
your mouse over that cell and then typing the digit. Typing anything other
than a digit will erase the cell.
Play sudoku now or read on for some tips on solving
sudoku.
Logical Steps
Most sudoku boards can be solved using logic to deduce where digits should
be placed. Use the fact that each digit can only be placed in each row,
column, and box once. This tutorial will walk you through solving an Extreme
sudoku which needs all the methods listed below to solve it (unless you feel
like guessing).
Pencil Marks
Pencil marks are small numbers written in a cell to indicate which numbers
could go there. You can always add or remove pencil marks in our sudoku
boards by using the mouse to select a +/- 1-9, or by hovering the mouse over
a square and typing + or - followed by the number to add or remove. You can
also turn on automatic pencil marks by checking the Pencil Marks box in the
Tools menu next to the sudoku grid. This will automatically update the pencil
marks for each cell (unless you override it).
We will turn on pencil marks for the tutorial, as they are very helpful in
seeing what is going on in the sudoku. Once you are experienced with sudoku
solving, you will probably want to avoid using the automatic pencil marks, as
they tend to make the easier sudoku boards too easy.
Eliminate Digits
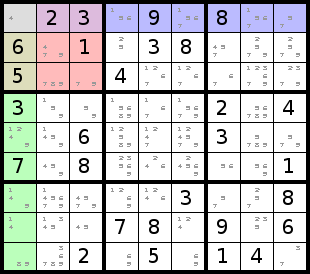 In the sudoku on the right, the first thing that jumps out at you might be the
solitary small 4 in the upper left cell. This cell can't be a 1 since there
is already a 1 in the box. It can't be a 2, 3, 8, or 9 because they are
already used in the row, and it can't be 5, 6, or 7 because they are already
used in the column. This leaves 4 as the only possibility. Now using the
same method, we can finish off the leftmost column.
In the sudoku on the right, the first thing that jumps out at you might be the
solitary small 4 in the upper left cell. This cell can't be a 1 since there
is already a 1 in the box. It can't be a 2, 3, 8, or 9 because they are
already used in the row, and it can't be 5, 6, or 7 because they are already
used in the column. This leaves 4 as the only possibility. Now using the
same method, we can finish off the leftmost column.
Eliminate Positions
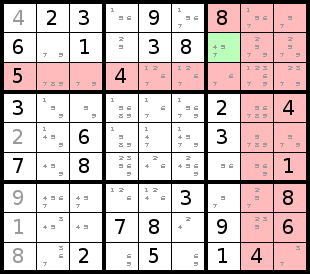 Now we will eliminate positions. The upper right box needs a 4. It
can't be placed in the second or third column because they already have 4s.
It can't go in the bottom row of the box because it has a 4. Since the top
left cell of the box is already an 8, that only leaves the middle left cell
of the box for a 4. With automatic pencil marks on, we can see this quicker
by noting that there is only one cell with a small 4 in it in that box.
Using this technique again we can place the 8 in the lower middle of the
upper left box and the 3 in the lower left corner of the middle box.
Now we will eliminate positions. The upper right box needs a 4. It
can't be placed in the second or third column because they already have 4s.
It can't go in the bottom row of the box because it has a 4. Since the top
left cell of the box is already an 8, that only leaves the middle left cell
of the box for a 4. With automatic pencil marks on, we can see this quicker
by noting that there is only one cell with a small 4 in it in that box.
Using this technique again we can place the 8 in the lower middle of the
upper left box and the 3 in the lower left corner of the middle box.
Partial Positions
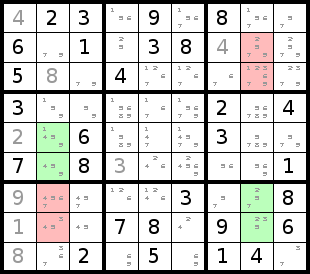 Sometimes you can't place a digit in a specific cell of the sudoku, but know
that it must go in one of two or three different positions. In the sudoku
board to the right, you can see that a 2 must go in one of the cells in the middle
column of the lower right box. That allows us to eliminate 2 as a possibility
for the lower two cells of the middle column of the upper right box.
Similarly the 4 in the left middle box can only go in the middle column, so we
can elimiate 4 as a possibility in the middle column cells of the lower left
box.
Sometimes you can't place a digit in a specific cell of the sudoku, but know
that it must go in one of two or three different positions. In the sudoku
board to the right, you can see that a 2 must go in one of the cells in the middle
column of the lower right box. That allows us to eliminate 2 as a possibility
for the lower two cells of the middle column of the upper right box.
Similarly the 4 in the left middle box can only go in the middle column, so we
can elimiate 4 as a possibility in the middle column cells of the lower left
box.
Tuples
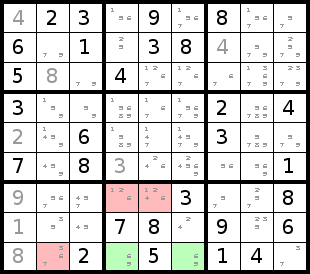 This is a generic name for pairs, triplets, etc. The bottom row of the
bottom middle box has two empty cells, both of which only have 6 and 9 as
possibilities. Because of this we know that one of them must be a 6 and the
other a 9. Though we don't know which goes where, we know that they will use
the 6 and 9 for the bottom row and the bottom middle box since they share
that row and box. Thus, we can eliminate 6 or 9 as a possibility in other
cells in that row or box. This technique can work with any two cells in the
same box, row, and/or column that share only two numbers between them. It
can also work for any three cells in the same box, row, or column that among
the three of them only have 3 different numbers (or 4 cells and 4 numbers, etc).
This is a generic name for pairs, triplets, etc. The bottom row of the
bottom middle box has two empty cells, both of which only have 6 and 9 as
possibilities. Because of this we know that one of them must be a 6 and the
other a 9. Though we don't know which goes where, we know that they will use
the 6 and 9 for the bottom row and the bottom middle box since they share
that row and box. Thus, we can eliminate 6 or 9 as a possibility in other
cells in that row or box. This technique can work with any two cells in the
same box, row, and/or column that share only two numbers between them. It
can also work for any three cells in the same box, row, or column that among
the three of them only have 3 different numbers (or 4 cells and 4 numbers, etc).
This allowed us to eliminate all positions but one for a six in the bottom
left box (and second column), so we will place a 6 in that remaining cell.
X-Wing
We now come to the most advanced technique covered in this tutorial - the
X-Wing. This involves finding to rows that have a number that can only go
in two different places in each row, and those places are in the same columns
of each row. Once we have found this, we know that the number must go in one
column in one of the rows and the other column in the other row. Since the
number will be used in both columns, it can be eliminated as a possibility
from all other cells in those columns. The same idea can be applied but
swapping rows and columns (which we will do to solve this sudoku).
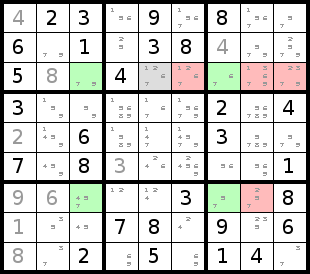 In the 3rd column, a 7 can go only in rows 3 or 7. Similarly, in the 7th
column, a 7 can go only in rows 3 or 7. So, if the 7 goes in row 3 of the 3rd
column, it cannot go in row 3 of the 7th column and must go in row 7 instead.
Likewise, if it goes in row 7 of the 3rd column it must go in row 3 of the 7th
column. Either way, the 7 will be used in both rows 3 and 7, so we can eliminate
it as a possibility for all other cells in those rows (the cells not in columns
3 or 7).
In the 3rd column, a 7 can go only in rows 3 or 7. Similarly, in the 7th
column, a 7 can go only in rows 3 or 7. So, if the 7 goes in row 3 of the 3rd
column, it cannot go in row 3 of the 7th column and must go in row 7 instead.
Likewise, if it goes in row 7 of the 3rd column it must go in row 3 of the 7th
column. Either way, the 7 will be used in both rows 3 and 7, so we can eliminate
it as a possibility for all other cells in those rows (the cells not in columns
3 or 7).
We can now place the 7 in the upper middle box, which allows us to finish off
the 5s in the top boxes, followed by the 2 in the upper right box and the 2 in
the 4th column (both have only one available cell). This last one allows us to
finish off the board through cells with only one available digit each.
Solution
Click here for the solution to this
sudoku.
Guessing
Often the above techniques are enough to finish the sudoku, as is the case
with this sudoku. In some sudokus, you may get to a point where you
can no longer logically deduce any more digits. When you get to this point, it
is necessary to pick a cell that you have reduced to two possibilities. Choose
one of the possibilities and work it out (you may want to mark all of the
changes you make with a color so you can undo them if your guess was wrong).
If you have picked the wrong one, you will eventually end up with a contradiction
- that is, to continue you will need to place two of the same digit in a row,
column, or box in the sudoku.
You can then go back and know that the other possibility was the correct one.
If, on the other hand, everything works out, then you have picked the correct
number for that cell and you have finished the sudoku. All of our sudokus
that require guessing are graded "Near Impossible." Any sudoku with a grade
other than Near Impossible is solvable using the above techniques.
 In the sudoku on the right, the first thing that jumps out at you might be the
solitary small 4 in the upper left cell. This cell can't be a 1 since there
is already a 1 in the box. It can't be a 2, 3, 8, or 9 because they are
already used in the row, and it can't be 5, 6, or 7 because they are already
used in the column. This leaves 4 as the only possibility. Now using the
same method, we can finish off the leftmost column.
In the sudoku on the right, the first thing that jumps out at you might be the
solitary small 4 in the upper left cell. This cell can't be a 1 since there
is already a 1 in the box. It can't be a 2, 3, 8, or 9 because they are
already used in the row, and it can't be 5, 6, or 7 because they are already
used in the column. This leaves 4 as the only possibility. Now using the
same method, we can finish off the leftmost column. Now we will eliminate positions. The upper right box needs a 4. It
can't be placed in the second or third column because they already have 4s.
It can't go in the bottom row of the box because it has a 4. Since the top
left cell of the box is already an 8, that only leaves the middle left cell
of the box for a 4. With automatic pencil marks on, we can see this quicker
by noting that there is only one cell with a small 4 in it in that box.
Using this technique again we can place the 8 in the lower middle of the
upper left box and the 3 in the lower left corner of the middle box.
Now we will eliminate positions. The upper right box needs a 4. It
can't be placed in the second or third column because they already have 4s.
It can't go in the bottom row of the box because it has a 4. Since the top
left cell of the box is already an 8, that only leaves the middle left cell
of the box for a 4. With automatic pencil marks on, we can see this quicker
by noting that there is only one cell with a small 4 in it in that box.
Using this technique again we can place the 8 in the lower middle of the
upper left box and the 3 in the lower left corner of the middle box. Sometimes you can't place a digit in a specific cell of the sudoku, but know
that it must go in one of two or three different positions. In the sudoku
board to the right, you can see that a 2 must go in one of the cells in the middle
column of the lower right box. That allows us to eliminate 2 as a possibility
for the lower two cells of the middle column of the upper right box.
Similarly the 4 in the left middle box can only go in the middle column, so we
can elimiate 4 as a possibility in the middle column cells of the lower left
box.
Sometimes you can't place a digit in a specific cell of the sudoku, but know
that it must go in one of two or three different positions. In the sudoku
board to the right, you can see that a 2 must go in one of the cells in the middle
column of the lower right box. That allows us to eliminate 2 as a possibility
for the lower two cells of the middle column of the upper right box.
Similarly the 4 in the left middle box can only go in the middle column, so we
can elimiate 4 as a possibility in the middle column cells of the lower left
box. This is a generic name for pairs, triplets, etc. The bottom row of the
bottom middle box has two empty cells, both of which only have 6 and 9 as
possibilities. Because of this we know that one of them must be a 6 and the
other a 9. Though we don't know which goes where, we know that they will use
the 6 and 9 for the bottom row and the bottom middle box since they share
that row and box. Thus, we can eliminate 6 or 9 as a possibility in other
cells in that row or box. This technique can work with any two cells in the
same box, row, and/or column that share only two numbers between them. It
can also work for any three cells in the same box, row, or column that among
the three of them only have 3 different numbers (or 4 cells and 4 numbers, etc).
This is a generic name for pairs, triplets, etc. The bottom row of the
bottom middle box has two empty cells, both of which only have 6 and 9 as
possibilities. Because of this we know that one of them must be a 6 and the
other a 9. Though we don't know which goes where, we know that they will use
the 6 and 9 for the bottom row and the bottom middle box since they share
that row and box. Thus, we can eliminate 6 or 9 as a possibility in other
cells in that row or box. This technique can work with any two cells in the
same box, row, and/or column that share only two numbers between them. It
can also work for any three cells in the same box, row, or column that among
the three of them only have 3 different numbers (or 4 cells and 4 numbers, etc).
 In the 3rd column, a 7 can go only in rows 3 or 7. Similarly, in the 7th
column, a 7 can go only in rows 3 or 7. So, if the 7 goes in row 3 of the 3rd
column, it cannot go in row 3 of the 7th column and must go in row 7 instead.
Likewise, if it goes in row 7 of the 3rd column it must go in row 3 of the 7th
column. Either way, the 7 will be used in both rows 3 and 7, so we can eliminate
it as a possibility for all other cells in those rows (the cells not in columns
3 or 7).
In the 3rd column, a 7 can go only in rows 3 or 7. Similarly, in the 7th
column, a 7 can go only in rows 3 or 7. So, if the 7 goes in row 3 of the 3rd
column, it cannot go in row 3 of the 7th column and must go in row 7 instead.
Likewise, if it goes in row 7 of the 3rd column it must go in row 3 of the 7th
column. Either way, the 7 will be used in both rows 3 and 7, so we can eliminate
it as a possibility for all other cells in those rows (the cells not in columns
3 or 7).